What is recursion?

 

java program

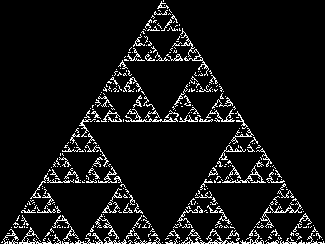
 Sierpinski's Triangle is a very famous fractal that's been seen by most advanced math students. This fractal consists of one large triangle, which contains an infinite amount of smaller triangles within. The infinite amount of triangles is easily understood if the fractal is zoomed in many levels. Each zoom will show yet more previously unseen triangles embedded in the visible ones.
Creating the fractal requires little computational power. Even simple graphing calculators can easily make this image. The fractal is created pixel by pixel, using random numbers; the fractal will be slightly different each time due to this. Although, if you were to run the program repeatedly, and allow each to use an infinite amount of time, the results would be always identical. No one has an infinite amount of time, but the differences in the finite versions are very small.
To generate this fractal, a few steps are involved. First, initial X and Y values should be chosen, either by the program or the user. The values used have little effect on the fractal. Regardless of what's chosen, the same triangle will be created. Next, the program must create a random number, between 0 and 1. Then, three possible routes can be taken.
  • If the random number is less then 1/3, then the following equations should be applied to X and Y.
    • xn = 0.5 * (xn-1 + 1)
    • yn = 0.5 * yn-1
  • If the random number is between 1/3 and 2/3, then these equations should be used.
    • xn = xn-1 * 0.5
    • yn = yn-1 * 0.5
  • If the number is greater than 2/3, the the following equations should be applied.
    • xn = 0.5 * (xn-1 + 0.5)
    • yn = 0.5 * (yn-1 + 1)

Now that X and Y have changed, the point should be plotted on the screen. Finally, loop back to the random number generation and start over again.
Only a few hundred iterations are needed to begin to see the triangles. A few thousand pixels will produce a good image.

 
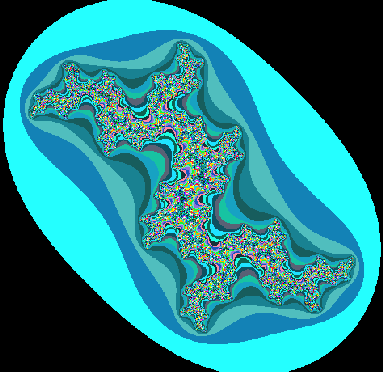The Julia set is closely related to the Mandelbrot set. For example, it is possible to determine whether a Julia set will be connected or a Cantor dust based on the Mandelbrot set. To calculate the Julia set, iterate the following function as you would the Mandelbrot function (that is, iterate until your maximum number of iterations is exceeded or until the absolute value of Z exceeds two):

Zn=Zn-12+C

Does the function look similar to something else you have seen? It is the same as the Mandelbrot function. The difference is that the value of C is fixed at an arbitrary value and the value of Z is the current point that you are plotting. If you want the set to be connected, the value for C should come from inside the Mandelbrot set. The most interesting patterns occur in values on the edge of the Mandelbrot set.

java program

 



A recursive definition is one that is defined in terms of itself. It must include a base case so that the recursion will eventually end.

 

 

Recursion in mathematics

Many mathematical functions have recursive definitions. Consider the factorial (!) operation on non-negative integers.

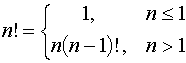
To illustrate,

     

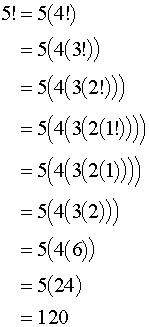
    public class Recursion
    {
    public static void main(String args[]) throws IOException
    {

            System.out.println(factorial(5));

    }

    int factorial(int n)
    {
      if(n < 1) // base case
        return 1;
      else
        return n * factorial(n-1); // recursive call
    }      

    }

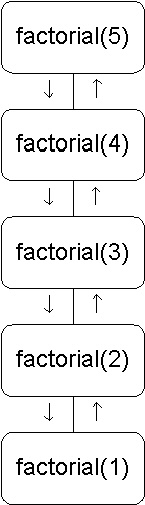
    Recursive Call Trace, Factorial Method

    Call traces help us understand the recursive process and analyze the complexity of recursive algorithms. Since each node of the factorial method’s call trace is O(1), the recursive invocation of factorial(n) is O(n).


     
     

     

    Recursion and mathematical induction

    Recall proofs by induction

      1. Show that the theorem is true for the smallest case. This can usually be done by inspection.
         
            ̃ basis
      2. Show that if the theorem is true for the basis cases, it can be extended to include the next case. If the theorem is true for the case k=n-1, show that it is true for the case k=n.
    ̃Inductive hypothesis assumes that the theorem is true for the case k=n-1. Similarity with recursive programming
      1. The base case of a recursive method is the case that can be solved without a recursive call.
      2. For the general (non-base) case, k=n, we assume that the recursive method works for k=n-1.

     

    Dangers of recursion: infinite regress

    Consider the following poorly designed implementation of the factorial method:

    int factorial(int n)
    {
        System.out.println("factorial("+n+") called");
        if(n == 1)
            return 1;
        else
            return n * factorial(n-1);
    }     What if we called this method with an argument of 0? We would see the following console output. factorial(0) called
    factorial(-1) called
    factorial(-2) called
    :
    factorial(-9999) called     … and so on, until a stack overflow occurs. This phenomenon is known as infinite regress and is a real danger of recursive programming. To avoid infinite regress, follow these two rules.
    1. Take special care to ensure that the base case is properly implemented.
    2. Make sure that each subsequent recursive call represents progress toward the base case

    Dangers of recursion: redundant calculations

    Consider the Fibonacci number sequence, defined as

                  

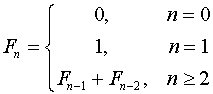
     The sequence: {0,1,1,2,3,5,8,13,...}

    where n is a non-negative integer. A method to generate Fibonacci numbers can be implemented recursively.

    public static int fib(int n)

    {
    if(n <= 1) return n; //base case
    else return fib(n-1) + fib(n-2);
    }

         Consider now the call trace for n=5.

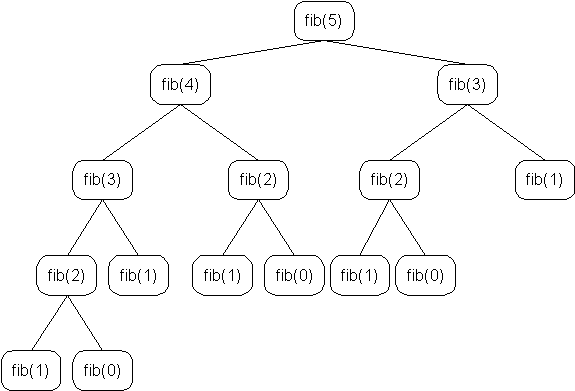
    Note the redundant calculations: 3 calls to fib(0), 5 calls to fib(1), and so on. Each recursive call does more and more redundant work, resulting in exponential growth.

     

    Mutual recursion

    So far we have only considered recursive methods that call themselves. Another type of recursion involves methods that cyclically call each other. This is known as cyclical or mutual recursion. In the following example, methods A and B are mutually recursive.
     
     
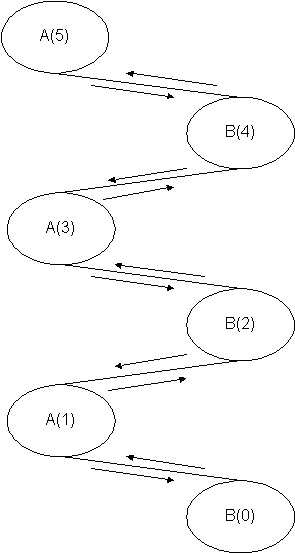    void A(int n)
    { 
      if (n <= 0) return;
      n--;
      B(n);
    }
     
     

    void B(int n)
    {
      if (n <= 0) returnl
      n--;
      A(n);
    }

     


     
     

    Divide-and-conquer recursion




    One of the more effective uses of recursion is through a class of algorithms known as divide and conquer.

    Divide – Smaller problems (subproblems) are solved recursively (except, of course, for the base case). Conquer – The solution to the original problem is then formed from solutions to the subproblems.

     

    Towers of Hanoi

    At a remote temple somewhere in Asia, a group of monks is working to move 64 disks from the leftmost peg (peg A) to the rightmost peg (peg C). After all 64 disks have been moved, the universe will dissolve! When will this happen if each disk takes 1 second to move?

    Rules of the puzzle:

    10-disk illustration

     

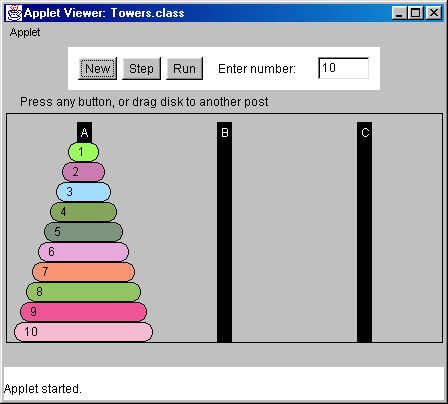
    Towers of Hanoi (2)

    Consider the n=4 subproblem.

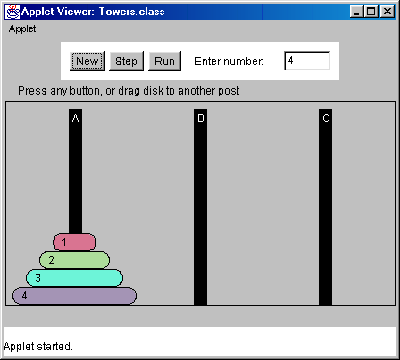
    Step 1: move 3 disks from peg A to peg B

     

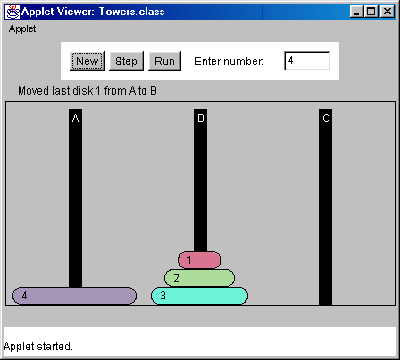
    Towers of Hanoi (3)

    Step 2: move 1 disk from peg A to peg C

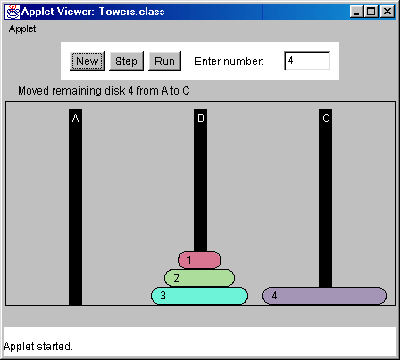
    Step 3: move 3 disks from peg B to peg C

     

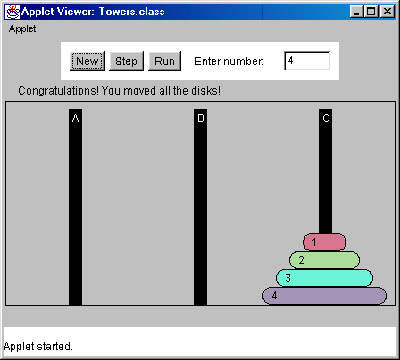
    Towers of Hanoi (4)

     public static void tower(int n, char start, char finish, char spare)
    {
      if (n<=1)
        System.out.println("Moving a disk from peg " + start +" to peg " +
                          finish);
      else
      {
        tower(n-1,start,spare,finish);
        System.out.println("Moving a disk from peg " + start +" to peg " +
                            finish);
       tower(n-1,spare,finish,start);
      }
    }
     

    Note that the solution to this problem is a divide-and-conquer algorithm. Calling the above method with n=4, i.e., tower(4,'A','C','B') yields the following result.

    Moving a disk from peg A to peg B
    Moving a disk from peg A to peg C
    Moving a disk from peg B to peg C
    Moving a disk from peg A to peg B
    Moving a disk from peg C to peg A
    Moving a disk from peg C to peg B
    Moving a disk from peg A to peg B
    Moving a disk from peg A to peg C
    Moving a disk from peg B to peg C
    Moving a disk from peg B to peg A
    Moving a disk from peg C to peg A
    Moving a disk from peg B to peg C
    Moving a disk from peg A to peg B
    Moving a disk from peg A to peg C
    Moving a disk from peg B to peg C
    Towers of Hanoi (5)

    Call trace for n=4:

    numbers inside nodes are n, start, finish

     

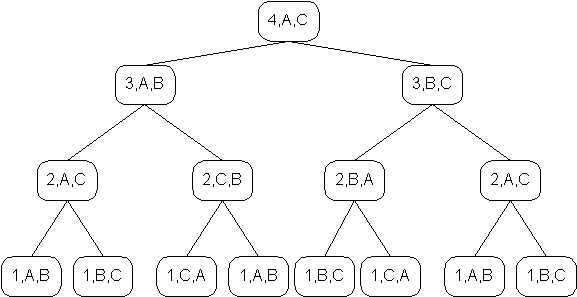
    Number of moves = 1 + 2 + 4 + 8.

    For n=64, number of moves = 264-1 @ 1.844´ 1019.

    Recall that one move takes one second.

    ̃ Time left in universe = 1.844´ 1019 seconds = 5.85´ 1011 years.

    Astronomers estimate the present age of the universe to be 20 billion (2´ 1010) years.

     

    ASSIGNMENT

    1. run the examples above

    2. what is the highest value of a factorial before it crashes

    3. what is the highest value of the towers of hanoi before it crashes

    4. send the program and rem out the crashed values.

    5. run the sierpinski triangle