loops

	Sign In Sign-Up

loops

Exercise 1 --- Adding up Integers

Write a program that adds up integers that the user enters. First the programs asks how many numbers will be added up. Then the program prompts the user for each number. Finally it prints the sum.

How many integers will be added:
5
Enter an integer:
3
Enter an integer:
4
Enter an integer:
-4
Enter an integer:
-3
Enter an integer:
7

The sum is 7

Be careful not to add the number of integers (in the example, 5) into the sum.

Exercise 2

Write a program that computes the following sum:

sum = 1.0/1 + 1.0/2 + 1.0/3 + 1.0/4 + 1.0/5 + .... + 1.0/N

N will be an integer limit that the user enters.

Enter N
4

Sum is: 2.08333333333

Exercise 3

Write a program that computes the standard deviation of a set of floating point numbers that the user enters. First the user will say how many numbers N are to follow. Then the program will ask for and read in each floating point number. Finally it will write out the standard deviation. The standard deviation of a set of numbers X_i is:

SD = Math.sqrt( avgSquare - avg² )

Here, avg is the average of the N numbers, and avg² is its square.

avgSquare is the average of X_i * X_i. In other words, this is the average of the squared value of each floating point number.

For example, if N = 4, say the numbers were:

X_i X_i * X_i

2.0 4.0

3.0 9.0

1.0 1.0

2.0 4.0

----- ------

sum 8.0 18.0

	X_i	X_i * X_i
	2.0	4.0
	3.0	9.0
	1.0	1.0
	2.0	4.0
	-----	------
sum	8.0	18.0

then

avg = 8.0/4 = 2.0
avg² = 4.0

avgSquare = 18.0/4 = 4.5

SD = Math.sqrt( 4.5 - 4.0 ) = Math.sqrt( .5 ) = 0.7071067812

To do this you will need to do several things inside the loop body for each floating point value as it comes in: add it to a sum, square it and add it to a sum of squares. Then after the loop is finished apply the formula.

Exercise 4 --- In-range Adder

Write a program that asks the user for the low and high integer in a range of integers. The program then asks the user for integers to be added up. The program computes two sums:

The sum of integers that are in the range (inclusive),
and the sum of integers that are outside of the range.

The user signals the end of input with a 0.

In-range Adder
Low end of range:
20
High end of range:
50
Enter data:
21
Enter data:
60
Enter data:
49
Enter data:
30
Enter data:
91
Enter data:
0
Sum of in range values: 100
Sum of out of range values: 151

Exercise 5--- Area of Rectangles

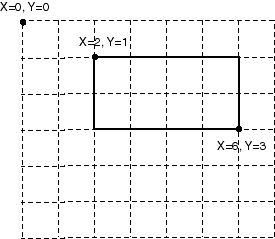
A computer aided design program expects users to enter the coordinates two corners for each of several of rectangles (see diagram.) The sides of the rectangles are assumed to be parallel to the X and Y axes. The coordinates of each corner is entered as a pair of integers, first the X coordinate and then the Y coordinate. The origin of the coordinate system (0,0) is in the upper left, so Y increases going downward, and X increases to the right.

For each rectangle, the program calculates and writes out the height, the width, and the area of the rectangle. The two corners entered for each rectangle must be diagonally opposite (upper left and lower right, or upper right and lower left), but which choice is made for each rectangle is up to the user. The user can enter the corners in any order. Height and width are always positive (the program will have to adjust its calculations so that this is true.)

The program ends gracefully when the user enters corners which cannot be those of a rectangle (either the height is zero, the width is zero, or both.)

first corner (x1,y1)

second corner (x2,y2)

width = x2-x1

height = y2-y1

area = width x height

Computer Aided Design Program
First corner X coordinate:
100
First corner Y coordinate:
100
Second corner X coordinate:
250
Second corner Y coordinate
200
Width:  150  Height: 100   Area: 15000

First corner X coordinate:
250
First corner Y coordinate:
200
Second corner X coordinate:
100
Second corner Y coordinate
100
Width:  150  Height: 100   Area: 15000

First corner X coordinate:
100
First corner Y coordinate:
200
Second corner X coordinate:
250
Second corner Y coordinate
100
Width:  150  Height: 100   Area: 15000

First corner X coordinate:
100
First corner Y coordinate:
100
Second corner X coordinate:
100
Second corner Y coordinate
100
Width:  0  Height: 0   Area: 0

finished

Exercise 6 --- Drug Potency

A certain drug looses 4% of its effectivness every month it is in storage. When its effectiveness is below 50% it is considered expired and must be discarded. Write a program that determines how many months the drug can remain in storage.

month: 0        effectiveness: 100.0
month: 1        effectiveness: 96.0
month: 2        effectiveness: 92.16
month: 3        effectiveness: 88.47359999999999
month: 4        effectiveness: 84.93465599999999
month: 5        effectiveness: 81.53726975999999
month: 6        effectiveness: 78.27577896959998
month: 7        effectiveness: 75.14474781081599
month: 8        effectiveness: 72.13895789838334
month: 9        effectiveness: 69.253399582448
month: 10       effectiveness: 66.48326359915008
month: 11       effectiveness: 63.82393305518407
month: 12       effectiveness: 61.27097573297671
month: 13       effectiveness: 58.82013670365764
month: 14       effectiveness: 56.46733123551133
month: 15       effectiveness: 54.20863798609088
month: 16       effectiveness: 52.04029246664724
month: 17       effectiveness: 49.95868076798135 DISCARDED